GPU programozás és párhuzamos rendszerek

A jelenlegi grafikus kártyák (GPU) nagy teljesítményű párhuzamos rendszerek (sok száz processzor és 1 teraflopnál nagyobb teljesítmény), amelyeket nem csupán a képszintézisben, hanem általános célú számításigényes feladatokban is fel lehet használni (lásd gpgpu.org). A GPU processzortömbjét C-szerű programozási nyelveken lehet programozni (Cg, HLSL, CUDA, OpenCL, stb.), de a hatékony alkalmazáshoz a párhuzamos programozás és a nagy teljesítményű számítási algoritmusok (HPC) elveit is el kell sajátítani.

A tárgy keretében a GPU-t mint általános célú párhuzamos programozási eszközt mutatjuk be különböző programozási környezetek (API-k) felhasználásával, és a hallgatók konkrét példákon keresztül tanulhatják meg ezen eszközök programozási módszereit. Az órákat laborban tartjuk, hogy a tanultakat rögtön alkalmazzuk is. 

A tárgyra regisztrált hallgatók számára elektronikusan hozzáférhető jegyzetek:

Szirmay-Kalos, Szécsi: GPGPU: General Purpose Computing on Graphics Processing Units. (in Algorithms of Informatics), mondAt Kiadó, 2011.

Szirmay-Kalos, Szécsi: GPU-Based Techniques for Global Illumination Effects, Morgan and Claypool Publishers, 2008.

Tematika:

1. A GPU története, fejlődési lépései. Fix-funkciójú csővezeték, képszintézis API-k programozható csúcspont, geometria és  pixel árnyalóval. A beépített elemek funkciói (raszterizáció, mélység teszt, alfa összemosás).

Labor: Ismerkedés a fejlesztő eszközzel, egyszerű grafikus programok készítése.

2. A GPU mint vektorprocesszor és mint stream-processzor.  OpenGL/GLSL API felépítése és használata.

Labor: Képfeldolgozási műveletek, szűrés, éldetektálás, mélységélesség párhuzamos megvalósítása. Mandelbrot halmaz rajzolás.

3. GPU programozás a vektorprocesszor modellen túl. SIMD és MIMD párhuzamos programozás. Iteratív algoritmusok hatékony megvalósítása.

Labor: Konvolúció szeparábilis függvényekkel. Fizikai szimuláció, a hullámegyenlet megoldása.

4. Szórás és gyűjtés típusú algoritmusok. Összetett képfeldologzási műveletek hatékony megvalósítása.

Labor: Hisztogram generálás és transzformációk. Tone-mapping.

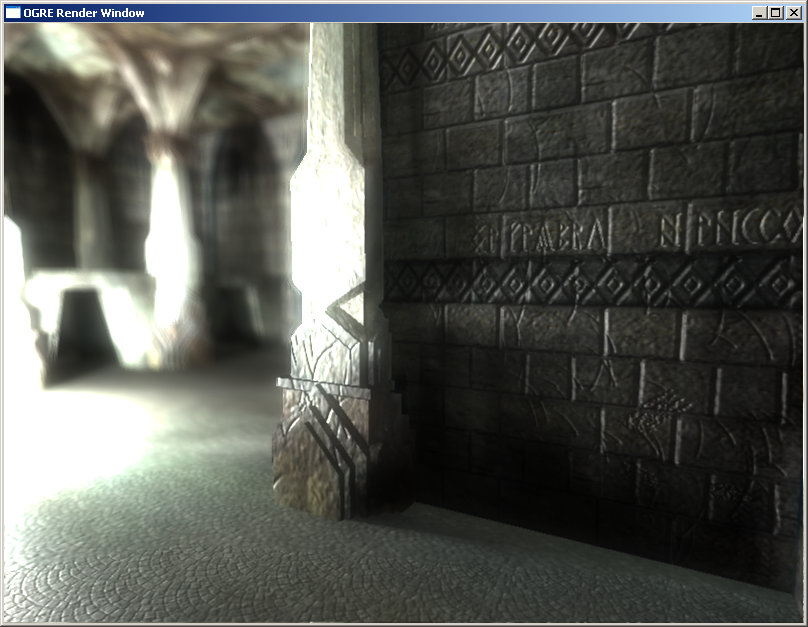
5. Sugárkövetés a GPU-n. A klasszikus rekurzív sugárkövetés jól párhuzamosítható probléma, azonban a GPU-n történő implementációhoz figyelembe kell venni az architektúrából fakadó korlátokat. Az előadás keretében áttekintjük a rekurzív sugárkövetés algoritmusát és a GPU-n történő implementáció kulcskérdéseit.

Labor: Egyszerű sugárkövető program megvalósítása.

6. Rekurzív algoritmusok. A grafikus hardver működéséből adódóan a rekurzió megoldása körültekintést igényel. Az előadás keretében bemutatjuk a rekurzív algoritmusok implementálásának két módszerét. Egyik lehetséges megoldás a textúrák esetén alkalmazott MipMap módszer használata a rekurzióra. Másik lehetőségünk a grafikus csővezeték geometria árnyalójának a használata.

Labor: Labirintus generálás és bejárás.

7. Beveztés az OpenCL általános célú GPGPU programozási környezetbe. Az előadás keretében bemutatjuk az OpenCL szabvány alapvető koncepcióit, a masszívan práhuzamos architektúra működtetéséhez szükséges infrastruktúrát.

Labor: Tőzsdei opcióárazás, statisztikai műveletek GPU-n.

8. Az OpenCL keretrendszer használata. Egy mintaprogramon keresztül áttekintjük egy egyszerű OpenCL program felépítését és a párhuzamos környezet használatát.

Labor: Ismerkedés az OpenCL-el. Párhuzamos modellek, függvény kiértékelés.

9. Lineáris egyenletrendszerek megoldása. Gauss-Jordan elimináció, Jakobi iterációs megoldás. A mátrix vektor szorzás optmalizálása párhuzamos architektúrára.

Labor: Lineáris egyenletrendszer megoldó program.

10. Monte Carlo módszerek a GPU-n. Az előadás keretében áttekintjük a Monte Carlo módszerek elméleti hátterét néhény egyszerű példán keresztül. Egyszerű véletlenszám generátorok felépítése és minőség vizsgálata.

Labor: Véletlenszám generálás, Monte Carlo integrálás.

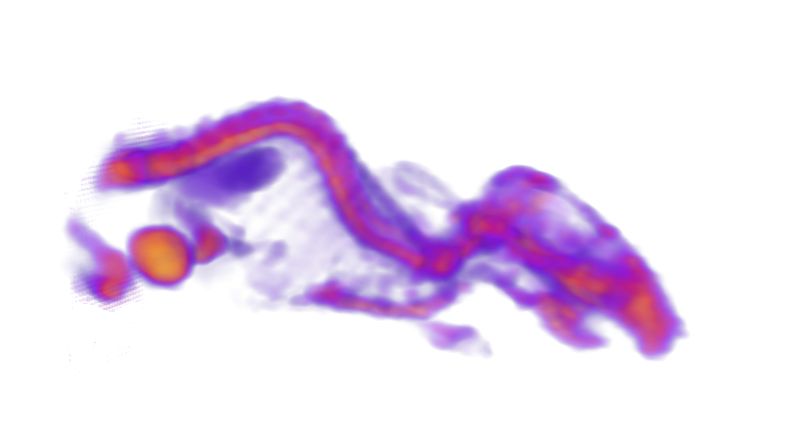
11. Monte Carlo szimuláció a GPU-n. Többszörös szóródás szimulációja inhomogén közegben, a szimuláció eredményének megjelenítése térfogat vizualizációs módszerrel.

Labor: Monte Carlo szimulációs program, térfogat vizualizáció.

12. Tomográfiás rekonstrukció. A gyógyászati gyakorlatban alkalmazott nem invazív képalkotó eljárások nagyon nagy méretű adatokon végzett nagy számításigényű algoritmusok használatát követelik meg. A rekonstrukció során a lehető legnagyobb pontosság mellett az idő tényező is kritikus, ezért a masszívan párhuzamos architektúrán futtatható algoritmusok napjainkban is elsődleges kutatási terület.

Labor: Egyszerű maximum expectation iterációs sémán alapuló rekonstrukciós program.

13. Folyadék szimuláció. A fizikai alapú szimuláció tipikusan nagy számításigényű probléma. Sok esetben az alkalmazott szimulációs algoritmus jól párhuzamosítható, ezért a grafikus hardver alkalmazása gyorsabb szimulációt vagy nagyobb problématér kezelését teszi lehetővé.

Labor: 2D áramlás szimuláció.

14. Az OpenCL környezet további lehetőségei. Szabványos bővítmény rendszer. Összehasonlítás egy másik elterjedt GPGPU környezettel a CUDA-val.

15. Házi feladatok bemutatása és beszámolók. 

Képek: