3D számítógépes geometria és alakzatrekonstrukció

A tárgy háromdimenziós pontfelhők, poligonhálók, görbék és felületek, valamint szilárd testek számítógépes reprezentációjával, legfontosabb algoritmusaival és ezek alkalmazásával foglalkozik. Az elméleti alapok mellett, a tudásanyag jól hasznosítható 3D-s számítógépes szoftver rendszerek fejlesztése és integrálása során, az alábbi területeken: számítógéppel segített tervezés, műszaki informatika, digitális alakzatrekonstrukció, 3D nyomtatás, virtuális valóság létrehozása.

Jelen tárgy a korábbi hasonló megnevezésű tárgyak (VIIIAV01, VIIIAV08, VIIIAV54) kibővített változata: (i) tágabb elméleti áttekintés, (ii) 3D-s modellezési gyakorlatok, (iii) geometriai algoritmusok implementációs  kérdései, (iv) ipari rendszerek demonstrációja. Új tematikai fejezet a 3D nyomtatás.

1. hét: 

• Bevezetés; vektorműveletek és lineáris algebra alapismeretek; görbék differenciálgeometriája
• Felületek differenciálgeometriája; az implicit és parametrikus reprezentáció összehasonlítása

2-4. hét:

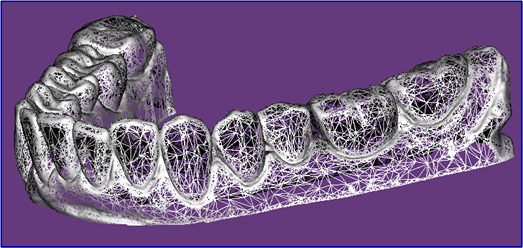
• Háromszöghálók 2D-ben: Voronoi diagram, Delaunay háromszögelés; háromszöghálók létrehozása 3D-ben nagyméretű pontfelhők alapján; implicit és parametrikus felületek háromszögelése
• Háromszöghálók egyszerűsítése; progresszív háromszöghálók; normálvektorok és görbületek becslése
• 3D modellezés: a ParaView rendszer - háromszöghálók és volumetrikus adatok megjelenítése és grafikus kiértékelése
• Háromszögháló algoritmusok számítógépes implementációja

5-8. hét:

• Polinomiális interpoláció; Bernstein polinomok; Bézier görbék és tulajdonságaik; egyszerű algoritmusok; Bézier felületek és tulajdonságaik
• B-spline görbék, csomópontok és bázisfüggvények; poláris forma; kontrollpoligonok; egyszerű algoritmusok;  tulajdonságok; B-spline felületek
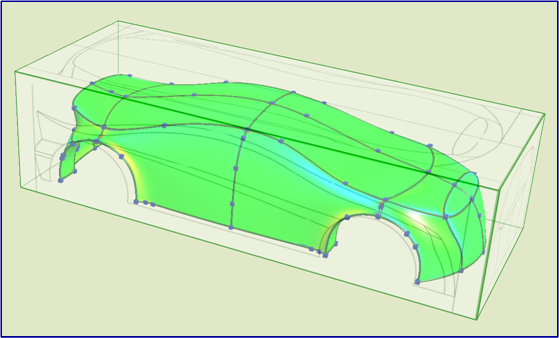
• Interpoláló felületek: Coons (transzfinit) felületek; általános n-oldalú felület reprezentációk
• Demó: Görbeháló alapú formatervezés (Sketches rendszer)
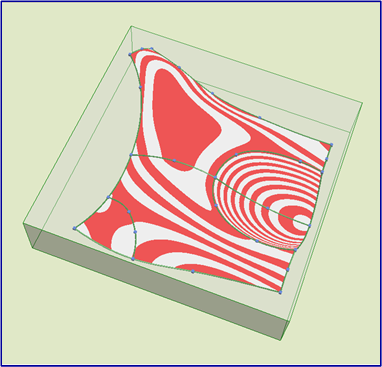
• Felosztásos felületek
• 3D modellezés: a Blender rendszer - görbék, felületek, poliéderek modellezése
• Görbe és felület algoritmusok számítógépes implementációja

9-11. hét:

• Procedurális (CSG) és kiértékelt (B-rep) reprezentáció, Euler szabály, regularizált halmazműveletek, határoló elem adatstruktúra
• Demó: tömör testek parametrikus modellezése (SolidWorks rendszer)
• Algoritmusok: görbeinterpoláció; felület-felület metszések; eltolásos (offset) felületek; lekerekítő felületek
• 3D nyomtatás; additív megmunkáló eljárások; geometriai követelmények

12-14. hét:

• A digitális alakzatrekonstrukció célja és folyamata; 3D-s méréstechnika
• Egyszerű implicit görbék és felületek illesztése
• 3D-s poligonhálók szegmentálása: tartománynövesztés, direkt szegmentáció, Morse szegmentáció

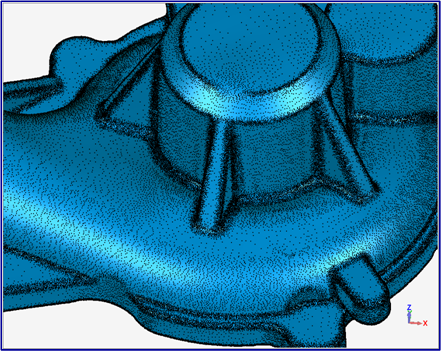
• Sűrű ponthalmazok közelítése parametrikus görbék és felületek segítségével; paraméterezés, gyenge tartópontok kizárása

• Demó: Digitális alakzatrekonstrukció a gyakorlatban (Geomagic Studio rendszer)

A tantárgy nagyobb része elméleti előadásokon kerül ismertetésre. A gyakorlatokon háromszöghálók, illetve szabadformájú görbék és felületek implementációs kérdéseivel foglalkozunk. Lehetőség nyílik egyszerű problémák megoldására és 3D-s modellezési gyakorlatok végrehajtására nyitott forrású rendszerek használatával. Több ipari rendszert is demonstrálunk a 3D-s felület- és testmodellezés, valamint a digitális alakzatrekonstrukció területéről.